In algebraic topology, a branch of mathematics, the (singular) homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways. Intuitively, it helps determine what part of an absolute homology group comes from which subspace.
Given a subspace  , one may form the short exact sequence
, one may form the short exact sequence

where  denotes the singular chains on the space X. The boundary map on
denotes the singular chains on the space X. The boundary map on  descendsa to
descendsa to  and therefore induces a boundary map
and therefore induces a boundary map  on the quotient. If we denote this quotient by
on the quotient. If we denote this quotient by  , we then have a complex
, we then have a complex

By definition, the nth relative homology group of the pair of spaces  is
is

One says that relative homology is given by the relative cycles, chains whose boundaries are chains on A, modulo the relative boundaries (chains that are homologous to a chain on A, i.e., chains that would be boundaries, modulo A again).[1]
The above short exact sequences specifying the relative chain groups give rise to a chain complex of short exact sequences. An application of the snake lemma then yields a long exact sequence

The connecting map  takes a relative cycle, representing a homology class in
takes a relative cycle, representing a homology class in  , to its boundary (which is a cycle in A).[2]
, to its boundary (which is a cycle in A).[2]
It follows that  , where
, where  is a point in X, is the n-th reduced homology group of X. In other words,
is a point in X, is the n-th reduced homology group of X. In other words,  for all
for all  . When
. When  ,
,  is the free module of one rank less than
is the free module of one rank less than  . The connected component containing
. The connected component containing  becomes trivial in relative homology.
becomes trivial in relative homology.
The excision theorem says that removing a sufficiently nice subset  leaves the relative homology groups
leaves the relative homology groups  unchanged. If
unchanged. If  has a neighbourhood
has a neighbourhood  in
in  that deformation retracts to
that deformation retracts to  , then using the long exact sequence of pairs and the excision theorem, one can show that
, then using the long exact sequence of pairs and the excision theorem, one can show that  is the same as the n-th reduced homology groups of the quotient space
is the same as the n-th reduced homology groups of the quotient space  .
.
Relative homology readily extends to the triple  for
for  .
.
One can define the Euler characteristic for a pair  by
by

The exactness of the sequence implies that the Euler characteristic is additive, i.e., if  , one has
, one has

The  -th local homology group of a space
-th local homology group of a space  at a point
at a point  , denoted
, denoted

is defined to be the relative homology group  . Informally, this is the "local" homology of
. Informally, this is the "local" homology of  close to
close to  .
.
Local homology of the cone CX at the origin
[edit]One easy example of local homology is calculating the local homology of the cone (topology) of a space at the origin of the cone. Recall that the cone is defined as the quotient space

where  has the subspace topology. Then, the origin
has the subspace topology. Then, the origin  is the equivalence class of points
is the equivalence class of points ![{\displaystyle [X\times 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7a4976c408c9d50777ca3399aa2bd83735c7df) . Using the intuition that the local homology group
. Using the intuition that the local homology group  of
of  at
at  captures the homology of
captures the homology of  "near" the origin, we should expect this is the homology of
"near" the origin, we should expect this is the homology of  since
since  has a homotopy retract to
has a homotopy retract to  . Computing the local homology can then be done using the long exact sequence in homology
. Computing the local homology can then be done using the long exact sequence in homology

Because the cone of a space is contractible, the middle homology groups are all zero, giving the isomorphism

since  is contractible to
is contractible to  .
.
In algebraic geometry
[edit]Note the previous construction can be proven in algebraic geometry using the affine cone of a projective variety  using Local cohomology.
using Local cohomology.
Local homology of a point on a smooth manifold
[edit]Another computation for local homology can be computed on a point  of a manifold
of a manifold  . Then, let
. Then, let  be a compact neighborhood of
be a compact neighborhood of  isomorphic to a closed disk
isomorphic to a closed disk  and let
and let  . Using the excision theorem there is an isomorphism of relative homology groups
. Using the excision theorem there is an isomorphism of relative homology groups

hence the local homology of a point reduces to the local homology of a point in a closed ball  . Because of the homotopy equivalence
. Because of the homotopy equivalence

and the fact

the only non-trivial part of the long exact sequence of the pair  is
is

hence the only non-zero local homology group is  .
.
Just as in absolute homology, continuous maps between spaces induce homomorphisms between relative homology groups. In fact, this map is exactly the induced map on homology groups, but it descends to the quotient.
Let  and
and  be pairs of spaces such that
be pairs of spaces such that  and
and  , and let
, and let  be a continuous map. Then there is an induced map
be a continuous map. Then there is an induced map  on the (absolute) chain groups. If
on the (absolute) chain groups. If  , then
, then  . Let
. Let

be the natural projections which take elements to their equivalence classes in the quotient groups. Then the map  is a group homomorphism. Since
is a group homomorphism. Since  , this map descends to the quotient, inducing a well-defined map
, this map descends to the quotient, inducing a well-defined map  such that the following diagram commutes:[3]
such that the following diagram commutes:[3]
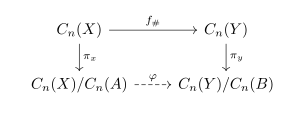
Chain maps induce homomorphisms between homology groups, so  induces a map
induces a map  on the relative homology groups.[2]
on the relative homology groups.[2]
One important use of relative homology is the computation of the homology groups of quotient spaces  . In the case that
. In the case that  is a subspace of
is a subspace of  fulfilling the mild regularity condition that there exists a neighborhood of
fulfilling the mild regularity condition that there exists a neighborhood of  that has
that has  as a deformation retract, then the group
as a deformation retract, then the group  is isomorphic to
is isomorphic to  . We can immediately use this fact to compute the homology of a sphere. We can realize
. We can immediately use this fact to compute the homology of a sphere. We can realize  as the quotient of an n-disk by its boundary, i.e.
as the quotient of an n-disk by its boundary, i.e.  . Applying the exact sequence of relative homology gives the following:
. Applying the exact sequence of relative homology gives the following:

Because the disk is contractible, we know its reduced homology groups vanish in all dimensions, so the above sequence collapses to the short exact sequence:

Therefore, we get isomorphisms  . We can now proceed by induction to show that
. We can now proceed by induction to show that  . Now because
. Now because  is the deformation retract of a suitable neighborhood of itself in
is the deformation retract of a suitable neighborhood of itself in  , we get that
, we get that  .
.
Another insightful geometric example is given by the relative homology of  where
where  . Then we can use the long exact sequence
. Then we can use the long exact sequence

Using exactness of the sequence we can see that  contains a loop
contains a loop  counterclockwise around the origin. Since the cokernel of
counterclockwise around the origin. Since the cokernel of  fits into the exact sequence
fits into the exact sequence

it must be isomorphic to  . One generator for the cokernel is the
. One generator for the cokernel is the  -chain
-chain ![{\displaystyle [1,\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e43e5f05e3352d73946cdde772514d692a5d448) since its boundary map is
since its boundary map is
![{\displaystyle \partial ([1,\alpha ])=[\alpha ]-[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97012f5d7c46724fafe8eebabcd897064ef6d1b)
^ i.e., the boundary  maps
maps  to
to 
- Specific




































![{\displaystyle [X\times 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7a4976c408c9d50777ca3399aa2bd83735c7df)

















































![{\displaystyle [1,\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e43e5f05e3352d73946cdde772514d692a5d448)
![{\displaystyle \partial ([1,\alpha ])=[\alpha ]-[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97012f5d7c46724fafe8eebabcd897064ef6d1b)


